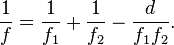Components of a sphero-cylindrical correction
Sphere component
Each power specification includes a spherical correction in diopters. Convergent powers are positive (e.g., +4.00 D) and condense light to correct for farsightedness (hyperopia) or allow the patient to read more comfortably (see presbyopia and binocular vision disorders). Divergent powers are negative (e.g., -3.75 D) and spread out light to correct for nearsightedness (myopia). If neither convergence nor divergence is required in the prescription, "plano" is used to denote a refractive power of zero.
Cylinder component
If a patient has an astigmatism, the patient needs two different correction powers in two different meridians (horizontally and vertically for example). This is specified by describing how the cylinder (the meridian that is most different from the spherical power) differs from the sphere power. Power evenly transitions between the two powers as you move from the meridian with the most convergence to the meridian with the least convergence or most divergence.
Some Ophthalmologists record in "plus cylinder notation" where the cylinder power is a number of diopters more convergent than the sphere power. That means the sphere power describes the most divergent meridian and the cylinder component describes the most convergent. Optometrists primarily use "minus cylinder notation" where the cylinder power is a number of diopters more divergent than the sphere component, however some use plus cyl. Thus the sphere power describes the most convergent meridian and the cylinder component describes the most divergent. (There is no difference in these forms of notation. They arise from the nature of the two professions and are easily converted between by people accustomed to working with sphero-cylindrical prescriptions. They are simply two ways to specify the same thing.)
Axis component
The axis defines the location of the sphere and cylinder powers. The sphere is almost always 90° from the cylinder. (This is regular astigmatism, which is by far more common than irregular astigmatism where separations are other than 90°). Vertical is the 90th meridian and horizontal is both zero and the 180th meridians. The axis is the meridian 90° away from the cylinder power. To rationalize this, think of a soft drink can, or other cylindrical object. Note how the curvature is 90° away from its axis (the line it would spin around if you were to roll it).
Since the cylinder and sphere powers almost always separated by 90°, the axis is also the location of the sphere component. If the lens is spherical (there is no cylinder component) then there is no need for an axis. A prescription like this is written with D.S. (diopters sphere) after the spherical power (e.g., -3.00 D.S.).
Sample prescription
So, a prescription of -1.00 +0.25 x 180 describes a lens that has a horizontal power of -1.00 D and a vertical power of -0.75. (The same prescription written in minus cylinder notation: -0.75 -0.25 x 090)
Other considerations
Single vision lenses correct for only distance or near vision. Patients with presbyopia or other disorders of accommodation often benefit from corrections for both distance and near vision (see Lens Types below). Infrequently, prism and base curve values may also be specified to correct for binocular vision disorders.
Over the counter correction
In some cases, mild farsightedness (hyperopia) can be treated with simple magnifying lenses or commodity reading glasses that can be purchased without a prescription. The magnifiers make the image of the object being viewed bigger so that it can be seen better. Over the counter readers are spherical corrective lenses of varying strengths (commonly +1.00 D to +4.00 D).
These treatments are not as tailored to the specific needs of the patient. A difference in refractive error or presence of astigmatism will not be accounted for. The use of improper corrective lenses may not help or could even exacerbate binocular vision disorders. Over the counter readers may not work for patients with significant refractive errors requiring distance correction (unless they are used in combination with contact lenses that correct distance vision). Eyecare professionals (optometrists and ophthalmologists) are trained to determine the specific corrective lenses that will provide the clearest, most comfortable and most efficient vision, avoiding double vision and maximizing binocularity. They can tell patients if over the counter corrective lenses are appropriate.
Lens types
Single vision
Single vision has the same optical focal point or correction over the entire area of the lens.
Single lenses in CR-39 plastic come finished and unfinished. An unfinished lens is ground at the time your prescription is filled and the base curve is called a compensated base curve due to the fact that the lab tech can use a wide range of base curves to make the lens. A finished lens on the other hand, has been made using the exact base curve to match the prescription and the natural curve of the eyeball and is therefore called a correct base curve.
Bifocal
Bifocal the upper part of the lens is generally used for distance vision, while the lower part is used for near vision. Usually, a segment line separates the two. Typically a person with myopia would have one section of a prescription lens that has a certain diverging power while another section of the lens would have a lower diverging power for close-up work. Similarly a person with hyperopia would have one section of the lens with a certain converging power and another section with a greater power for close-up work.
Trifocal
Trifocal lenses are similar to bifocals, except that the two focal areas are separated by a third middle area with intermediate focus correction, used for intermediate vision, e.g. computer distance. This lens type has two segment lines, dividing the three different correcting segments.
Progressive
Progressive or varifocal provide a smooth transition from distance correction to near correction, eliminating segment lines and allowing the viewing of all intermediate distances.
Adjustable focus
Adjustable or variable focus dynamically adjusts focal length to allow clear vision at any distance. It is especially useful for treating the loss of accommodation common in presbyopia.
Aspheric
Aspheric lenses are typically designed to give a thinner lens, and also distort the viewer's eyes less as seen by other people, producing better aesthetic appearance.[1] Older texts may refer to lenticular lens polynomial designs,[2] and advantages of curvatures that do not produce Scotoma, or a blind spot.
Plano
Some people with good natural eyesight like to wear eyeglasses as a style accessory, or want to change the appearance of their eyes using novelty contact lenses. For these people, no power or acuity correction is required. In this case the lens is simply a placeholder that does nothing, with equal parallel curved surfaces. This is referred to as a plano lens.
Lens optical profile
Common lens optical profiles

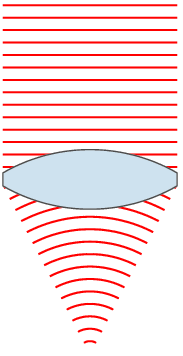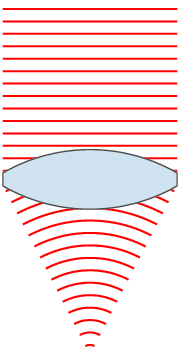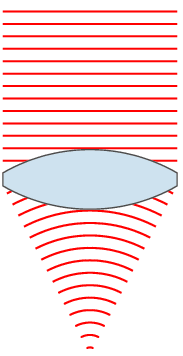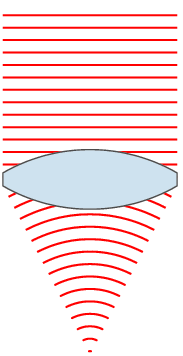
Although corrective lenses can be produced in many different profiles, the most common is ophthalmic or convex-concave. In an ophthalmic lens, both the front and back surface have a positive radius, resulting in a positive / convergent front surface and a negative / divergent back surface. The difference in curvature between the front and rear surface leads to the corrective power of the lens. In hyperopia and presbyopia a convergent lens is needed, therefore the convergent front surface overpowers the divergent back surface. For myopia the opposite is true: the divergent back surface is greater in magnitude than the convergent front surface.
The base curve (usually determined from the profile of the front surface of an ophthalmic lens) can be changed to result in the best optic and cosmetic characteristics across the entire surface of the lens. Optometrists may choose to specify a particular base curve when prescribing a corrective lens for either of these reasons. A multitude of mathematical formulas and professional clinical experience has allowed optometrists and lens designers to determine standard base curves that are ideal for most people.
A much more detailed web-published document with technical images and diagrams may be found here:
• Bifocals, Trifocals, and Progressive-Addition Lenses by H. Jay Wisnicki, M.D., Focal Points: Clinical Modules for Ophthalmologists, by the American Academy of Ophthalmologists, Volume 17, Number 6, June 1999 (Section 3 of 3)
Bifocals and trifocals
Bifocals and trifocals result in a more complex lens profile, compounding multiple spherical surfaces. The main lens is composed of two spherical surfaces, and the bifocal adds a third spherical segment, working with the back side spherical surface.
The bifocal spherical segment is called an add segment, but is cut into the lens in the manufacturing process and is not an actual separate piece of material glued onto main lens.
There are many profiles and sizes of segments and the method that they are combined with the distance corrective lens has to do with the lens material and segment type. Some examples include Flat top, Kryptok, Orthogon, Tillyer Executive, Ultex A.
The optical center of the bifocal may be placed on the lens surface or may hang off into empty space near the lens surface. Although the surface profile of a bifocal segment is spherical, it is often trimmed to have straight edges so that it is contained within a small region of the lens surface.
Progressive lens
The progressive addition lens (PAL, also commonly called a progressive lens) eliminates the line in bi/tri-focals and are very complex in their profile. They are a continuously variable parametric surface that begins using one spherical surface base curve and ends at another, with the radius of curvature continuously varying as the transition is made from one surface to the other.
Lens shape
Fashion eyeglasses that limit the lower part of the visual field. The wearer must tilt their head down to see through the lenses, rather than moving their eyes.
Corrective lenses can be produced in many different shapes, from a simple circular lens, to wide, squat rectangular fashion glasses, to full eye lenses that cover as much of the visual space as possible.
For lower power lenses, the wearer may choose a lens shape that is limiting in the corrective capability but which allows for trendy fashion shapes.
Higher power patients with naturally poor vision may opt for a larger full-eye lens simply because without the lens they can not see clearly, and a small lens leads to tunnel vision with blurriness in the surrounding space beyond the edges of the lens.
Bifocal, trifocal, and progressive lenses generally require a tall lens shape to accommodate the different bands of lens focus. If the lens is too squat these bands form very narrow strips, as if looking at the world through a clearly focused mailbox slot within the bands of focus.
Refractive index
In the UK and the US, the refractive index is generally specified with respect to the yellow He-d Fraunhofer line, commonly abbreviated as nd. Lens materials are classified by their refractive index, as follows:
• Normal index - 1.48 = nd < 1.54
• Mid-index - 1.54 = nd < 1.60
• High-index - 1.60 = nd < 1.74
• Very high index - 1.76 = nd
This is a general classification. Indexes of nd values that are = 1.60 can be, often for marketing purposes, referred to as high-index. Likewise, Trivex and other borderline normal/mid-index materials, may be referred to as mid-index.
Advantages of higher indices
• Thinner, sometimes lighter lenses (See below).
[Disadvantages of increased indices
• Lower Abbe number meaning, amongst other things, increased chromatic aberration.
• Poorer light transmission and increased backside and inner-surface reflections (see Fresnel reflection equation) increasing importance of anti-reflective coating.
• Manufacturing defects have more impact on optical quality[citation needed].
• Theoretically, off-axis optical quality degrades (oblique astigmatic error). In practice this degradation should not be perceptible - current frame styles are much smaller than they would have to be for these aberrations to be noticeable to the patient, the aberration occurring some distance away from the optical centre of the lens (off-axis).
Optical quality
Abbe number
Chromatic aberration caused by a convex lens
Prismatic color distortion shown with a camera set for nearsighted focus, and using -9.5 diopter eyeglasses to correct the camera's myopia.
Close-up of color shifting through corner of eyeglasses. The light and dark borders visible between color swatches do not exist.
Of all of the properties of a particular lens material, the one that most closely relates to its optical performance is its dispersion, which is specified by the Abbe number. Lower Abbe numbers result in the presence of chromatic aberration (i.e., color fringes above/below or to the left/right of a high contrast object), especially in larger lens sizes and stronger prescriptions (±4D or greater). Generally, lower Abbe numbers are a property of mid and higher index lenses that cannot be avoided, regardless of the material used. The Abbe number for a material at a particular refractive index formulation is usually specified as its Abbe value.
In practice, a change from 30 to 32 Abbe will not have a practically noticeable benefit, but a change from 30 to 47 could be beneficial for users with strong prescriptions that move their eyes and look ‘off-axis’ of optical center of the lens. Note that some users do not sense color fringing directly but will just describe 'off-axis blurriness'. Abbe values even as high as that of (Vd=45) produce chromatic aberrations which can be perceptible to a user in lenses larger than 40 mm in diameter and especially in strengths that are in excess of ±4D. At ±8D even glass (Vd=58) produces chromatic aberration that can be noticed by a user. Chromatic aberration is independent of the lens being of spherical, aspheric, or atoric design.
The eye’s Abbe number is independent of the importance of the corrective lens’s ABBE, since the human eye:
• Moves to keep the visual axis close to its achromatic axis, which is completely free of dispersion (i.e., to see the dispersion one would have to concentrate on points in the periphery of vision, where visual clarity is quite poor)
• Is very insensitive, especially to color, in the periphery (i.e., at retinal points distant from the achromatic axis and thus not falling on the fovea, where the cone cells responsible for color vision are concentrated. See: Anatomy and Physiology of the Retina.)
In contrast, the eye moves to look through various parts of a corrective lens as it shifts its gaze, some of which can be as much as several centimeters off of the optical center. Thus, despite the eye's dispersive properties, the corrective lens's dispersion cannot be dismissed. People who are sensitive to the effects of chromatic aberrations, or who have stronger prescriptions, or who often look off the lens’s optical center, or who prefer larger corrective lens sizes may be impacted by chromatic aberration. To minimize chromatic aberration:
• Try to use the smallest vertical lens size that is comfortable. Generally, chromatic aberrations are more noticeable as the pupil moves vertically below the optical center of the lens (e.g., reading or looking at the ground while standing or walking). Keep in mind that a smaller vertical lens size will result in a greater amount of vertical head movement, especially while performing activities that involve short and intermediate distance viewing, which could lead to an increase in neck strain, especially in occupations involving a large vertical field of view.
• Restrict the choice of lens material to the highest Abbe value at acceptable thickness. The oldest most basic commonly used lens materials also happen to have the best optical characteristics at the expense of corrective lens thickness (i.e., cosmetics). Newer materials have focused on improved cosmetics and increased impact safety, at the expense of optical quality. All lenses sold in USA pass the FDA ball-drop impact test, and depending on needed index these seem to currently have ‘best in class’ Abbe vs Index (Nd): Glass (2x weight of plastics) or CR-39 (2 mm vs. 1.5 mm thickness typical on newer materials) 58 @ 1.5, Sola Spectralite (47@1.53), Sola Finalite (43@1.6), and Hoya Eyry (36 @ 1.7). For impact resistance safety glass is offered at a variety of indexes at high Abbe number, but is still 2x the weight of plastics. Polycarbonate (Vd=30-32) is very dispersive, but has excellent shatter resistance. Trivex (Vd=43 @ 1.53), is also heavily marketed as an impact resistant alternative to Polycarbonate, for individuals who don’t need polycarbonate’s index. Trivex is also one of the lightest materials available.
• Use contact lenses in place of eyeglasses. A contact lens rests directly on the surface of the cornea and moves in sync with all eye movements. Consequently the contact lens is always directly aligned on center with the pupil and there is never any off-axis misalignment between the pupil and the optical center of the lens.
Power error (-D corrections for myopia)
Power error is the change in the optical power of a lens as the eye looks through various points on the area of the lens. Generally, it is least present at the optic center and gets progressively worse as one looks towards the edges of the lens. The actual amount of power error is highly dependent on the strength of the prescription as well as whether a best spherical form of lens or an optically optimal aspherical form was used in the manufacture of the lens. Generally, best spherical form lenses attempt to keep the ocular curve between four and seven diopters.
Lens induced oblique astigmatism (+D corrections for presbyopia)
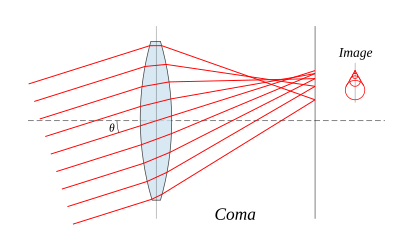
Effects of astigmatism
As the eye shifts its gaze from looking through the optical center of the corrective lens, the lens induced astigmatism value increases. In a spherical lens, especially one with a strong correction whose base curve is not in the best spherical form, such increases can significantly impact the clarity of vision in the periphery.
Minimizing power error and lens induced astigmatism
As corrective power increases, even optimally designed lenses will have distortion that can be noticed by a user. This particularly affects individuals that use the off-axis areas of their lenses for visually demanding tasks. For individuals sensitive to lens errors, the best way to eliminate lens induced aberrations is to use contact lenses. Contacts eliminate all these aberrations since the lens then moves with the eye.
Barring contacts, a good lens designer doesn’t have many parameters which can be traded off to improve vision. Index has little effect on error. Note that, chromatic aberration is often perceived as ‘blurry vision’ in the lens periphery giving the impression of power error, although this is actually due to color shifting. Chromatic aberration can be improved by using a material with improved ABBE. The best way to combat lens induced power error is to limit the choice of corrective lens to one that is in the best spherical form. A lens designer determines the best-form spherical curve using the Oswalt curve on the Tscherning ellipse. This design gives the best achievable optical quality and least sensitivity to lens fitting. A flatter base-curve is sometime selected for cosmetic reasons. Aspheric or atoric design can reduce errors induced by using a suboptimal flatter base-curve. They cannot surpass the optical quality of a spherical best-form lens, but can reduce the error induced by using a flatter than optimal base curve. The improvement due to flattening is most evident for strong farsighted lenses. High myopes (-6D) may see a slight cosmetic benefit with larger lenses. Mild prescriptions will have no perceptible benefit (-2D). Even at high prescriptions some high myope prescriptions with small lenses may not see any difference, since some aspheric lenses have a spherically designed center area for improved vision and fit.[1]
In practice, labs tend to produce pre-finished and finished lenses in groups of narrow power ranges to reduce inventory. Lens powers that fall into the range of the prescriptions of each group share a constant base curve. For example, corrections from -4.00D to -4.50D may be grouped and forced to share the same base curve characteristics, but the spherical form is only best for a -4.25D prescription. In this case the error will be imperceptible to the human eye. However, some manufacturers may further cost-reduce inventory and group over a larger range which will result in perceptible error for some users in the range who also use the off-axis area of their lens. Additionally some manufacturers may verge toward a slightly flatter curve. Although if only a slight bias toward plano is introduced it may be negligible cosmetically and optically. These optical degradations due to base-curve grouping also apply to aspherics since their shapes are intentionally flattened and then asphericized to minimize error for the average base curve in the grouping.
Cosmetics and weight
Reducing lens thickness
Note that the greatest cosmetic improvement on lens thickness (and weight) is had from choosing a frame which holds physically small lenses. The curves on the front and back of a lens are ideally formed with the specific radius of a sphere. This radius is set by the lens designer based on the prescription and cosmetic consideration. Selecting a smaller lens will mean less of this sphere surface is represented by the lens surface, meaning the lens will have a thinner edge (myopia) or center (hyperopia). A thinner edge reduces light entering into the edge, reducing an additional source of internal reflections.
Extremely thick lenses for myopia can be beveled to reduce flaring out of the very thick edge. Thick myopic lenses are not usually mounted in wire frames, because the thin wire contrasts against the thick lens, to make its thickness much more obvious to others.
Index can improve the lens thinness, but at a point no more improvement will be realized. For example, if an index and lens size is selected with center to edge thickness difference of 1 mm then changing index can only improve thickness by a fraction of this. This is also true with aspheric design lenses.
The lens's minimum thickness can also be varied. The FDA ball drop test sets the minimum thickness of materials. Glass or CR-39 requires 2.0 mm, but some newer materials only require 1.5 mm or even 1.0 mm minimum thickness.
Weight
Material density typically increases as lens thickness is reduced by increasing index. There is also a minimum lens thickness required to support the lens shape. These factors results in a thinner lens which is not lighter than the original. There are lens materials with lower density at higher index which can result in a truly lighter lens. These materials can be found in a material property table. Reducing frame lens size will give the most noticeable improvement in weight for a given material.
Facial distortion and social stigma
Eyeglasses for a high-diopter nearsighted or farsighted person cause a visible distortion of their face as seen by other people, in the apparent size of the eyes and facial features visible through the eyeglasses.
• For extreme nearsightedness the eyes appear small and sunken into the face, and the sides of the skull can be visible through the lens. This gives the wearer the appearance of having a very large or fat head in contrast with their eyes.
• For extreme farsightedness the eyes appear very large on the face, making the wearer's head seem too small.
Either situation can result in social stigma for children and adults due to apparent unattractiveness or uglyness of the wearer caused by these facial distortions. This can result in low self-esteem of the eyeglass wearer and lead to difficulty in making friends and developing relationships.
People with very high power corrective lenses can benefit socially from contact lenses because these distortions are minimized and their facial appearance to others is normal. Aspheric/atoric eyeglass design can also reduce minification and magnification of the eye for observers at some angles.
Lens materials
Optical crown glass (B270)
• Refractive index (nd): 1.52288
• Abbe value (Vd): 58.5
• Density: 2.55 g/cm³ (the heaviest corrective lens material in common use, today)
• UV cutoff: 320 nm
o Please note: Schott B270 is an optical glass used in precision optics. It is NOT an ophthalmic glass. Schott ophthalmic glass types are S-1 and S-3. The issue here is an incorrect value for UVA and UVB transmission, as well as other related product type issues. ***
Glass lenses have become less common in recent years due to the danger of shattering and their relatively high weight compared to CR-39 plastic lenses. They still remain in use for specialised circumstances, for example in extremely high prescriptions (currently, glass lenses can be manufactured up to a refractive index of 1.9) and in certain occupations where the hard surface of glass offers more protection from sparks or shards of material. If the highest Abbe value is desired, the only choices for common lens optical material are optical crown glass and CR-39.
Higher quality optical-grade glass materials exist (e.g., Borosilicate crown glasses such as BK7 (nd=1.51680 / Vd=64.17 / D=2.51 g/cm³), which is commonly used in telescopes and binoculars, and fluorite crown glasses such as Schott N-FK51A (nd=1.48656 / Vd=84.47 / D=3.675 g/cm³), which is 16.2 times the price of a comparable amount of BK7, and are commonly used in high-end camera lenses). However, one would be very hard pressed to find a laboratory that would be willing to acquire or shape custom eyeglass lenses, considering that the order would most likely consist of just two different lenses, out of these materials. Generally, Vd values above 60 are of dubious value, except in combinations of extreme prescriptions, large lens sizes, a high wearer sensitivity to dispersion, and occupations that involve work with high contrast elements (e.g., reading dark print on very bright white paper, construction involving contrast of building elements against a cloudy white sky, a workplace with recessed can or other concentrated small area lighting, etc.).
Plastic (CR-39)
• Refractive index (nd): 1.498 (standard)
• Abbe value (Vd): 59.3
• Density: 1.31 g/cm³
• UV cutoff: 355 nm
Plastic lenses are currently the most commonly prescribed lens, due to their relative safety, low cost, ease of production, and outstanding optical quality. The main drawbacks are the ease by which a lens can be scratched, and the limitations and costs of producing higher index lenses. CR-39 lenses are the exception to the plastics in that they have inherent scratch resistance.
Trivex
• Refractive index (nd): 1.532
• Abbe value (Vd): 43–45 (depending on licensing manufacturer)
• Density: 1.1 g/cm³ (the lightest corrective lens material in common use)
• UV cutoff: 380 nm
Trivex is a relative newcomer that possesses the UV blocking properties and shatter resistance of polycarbonate while at the same time offering far superior optical quality (i.e., higher Abbe value) and a slightly lower density. Its lower refractive index of 1.532 vs. polycarbonate's 1.586, however, may result in slightly thicker lenses. Along with polycarbonate and the various high-index plastics, Trivex is a lab favorite for use in rimless frames, due to the ease with which it can be drilled as well as its resistance to cracking around the drill holes. One other advantage that Trivex has over polycarbonate is that it can be easily tinted.
Polycarbonate
• Refractive index (nd): 1.586
• Abbe value (Vd): 30
• Density: 1.2 g/cm³
• UV cutoff: 385 nm
Polycarbonate is lighter weight than normal plastic. It blocks UV rays, is shatter resistant and is used in sports glasses and glasses for children and teenagers. Because polycarbonate is soft and will scratch easily, scratch resistant coating is typically applied after shaping and polishing the lens. Standard polycarbonate with an Abbe value of 30 is one of the worst materials optically, if chromatic aberration intolerance is of concern. Along with Trivex and the high-index plastics, polycarbonate is an excellent choice for rimless eyeglasses. Similar to the high-index plastics, polycarbonate has a very low Abbe value which may be bothersome to individuals sensitive to chromatic aberrations.
High-index plastics (polyurethanes)
• Refractive index (nd): 1.640–1.740
• Abbe value (Vd): 42–32 (higher indexes generally result in lower Abbe values)
• Density: 1.3–1.5 (g/cm³)
• UV cutoff: 380–400 nm
High-index plastics allow for thinner lenses. The lenses may not be lighter, however, due to the increase in density vs. mid- and normal index materials. Despite being popular with customers due to their thinner appearance, high-index lenses also suffer from a much higher level of chromatic aberrations due to their lower Abbe value. For people with strong prescriptions, the significant reduction in thickness may warrant the reduction in optical quality. Aside from thinness of the lens, another advantage of high-index plastics is their strength and shatter resistance, although not as shatter resistant as polycarbonate. This makes them another excellent choice for rimless eyeglasses.
Ophthalmic material property tables
Material, Plastic Index (Nd) ABBE (Vd) Specific Gravity (g/cm3) UVB/ UVA Reflected light (%) Minimum thickness typ/min (mm) Note
CR-39 Hard Resin 1.49 59 1.31 100% / 90% 7.97 ?/2.0
PPG Trivex (Average) 1.53 44 1.11 100% / 100% 8.70 ?/1.0 PPG, Augen, HOYA, Thai Optical, X-cel, Younger
SOLA Spectralite 1.54 47 1.21 100% / 98% 8.96 (also Vision 3456 (Kodak)?)
Essilor Ormex 1.56[1]
37 1.23 100% / 100% 9.52
Polycarbonate 1.586 30 1.20 100% / 100% 10.27 ?/1.5 Tegra (Vision-Ease) Airwear (Essilor) FeatherWates (LensCrafters)
MR-8 1.6 Plastic 1.6[2]
41 1.30 100% / 100% 10.43
MR-6 1.6 Plastic 1.6[3]
36 1.34 100% / 100% 10.57
Tokai MR-20 1.6 Plastic 1.60 42 1.30 100% / 100%
SOLA Finalite 1.60 42 1.22 100% / 100% 10.65
MR-7 1.67 Plastic 1.66 32 1.35 100% / 100% 12.26
MR-10 1.67 Plastic 1.66 32 1.37 100% / 100% 12.34
Nikon 4 Plastic NL4 1.67 32 1.35 100% / 100%
Hoya EYRY 1.70 36 1.41 100% / 100% 13.44 ?/1.5
MR-174 1.74 Plastic 1.73 33 1.47 100% / 100% 14.36 Hyperindex 174 (Optima)
Nikon 5 Plastic NL5 1.74 33 1.46 100% / 100%
Tokai 1.76 30 1.49 100% / 100%
Material, Glass Index (Nd) ABBE (Vd) Specific Gravity UVB/ UVA Reflected light (%) Minimum thickness typ/min (mm) Note
Crown Glass 1.525 59 2.54 79% / 20% 8.59
PhotoGray Extra 1.523 57 2.41 100% / 97% 8.59
1.6 Glass 1.604 40 2.62 100% / 61% 10.68 Zeiss Uropal, VisionEase, X-Cel
1.7 Glass 1.706 30 2.93 100% / 76% 13.47 Zeiss Tital, X-Cel, VisionEase, Phillips
1.8 Glass 1.800 25 3.37 100% / 81% 16.47 Zeiss Tital, X-Cell, Phillips, VisionEase,Zhong Chuan Optical(China)
1.9 Glass 1.893 31 4.02 100% / 76% 18.85 Zeiss Lantal,Zhong Chuan Optical(China)
Reflected light calculated using Fresnel reflection equation for normal waves against air on two interfaces. This is reflection without an AR coating.
Compilations of manufacturer material data can be found at opticampus, firstvisionmedia, and eyecarecontacts. Additional information on branding can be found at eyetopics.
Indices of refraction for a range of materials can be found in the List of indices of refraction.
Lens coatings
Main article: Optical coating
Anti-reflective
The effects of an anti-reflective coating applied (as seen on the bottom picture) as compared to regular eyeglass lens (notice how the reflection of the photographer in the top lens is clearly visible)
Main article: Anti-reflective coating
Anti-reflective coatings help to make the eye behind the lens more visible. They also help lessen back reflections of the white of the eye as well as bright objects behind the eyeglasses wearer (e.g., windows, lamps). Such reduction of back reflections increases the apparent contrast of surroundings. At night, anti-reflective coatings help to reduce headlight glare from oncoming cars, street lamps and heavily lit or neon signs.
One problem with anti-reflective coatings is that historically they have been very easy to scratch. Newer coatings, such as Crizal Alizé with its 5.0 rating and Hoya's Super HiVision with its 10.9 rating on the COLTS Bayer Abrasion Test (glass averages 12–14), try to address this problem by combining scratch resistance with the anti-reflective coating. They also offer a measure of dirt and smudge resistance, due to their hydrophobic properties (110° water drop contact angle for Super HiVision and 112° for Crizal Alizé).
Ultraviolet protection
A UV coating is used to reduce the transmission of light in the ultraviolet spectrum. UV-B radiation increases the likelihood of cataracts, while long term exposure to UV-A radiation can damage the retina. DNA damage from UV light is cumulative and irreversible. Some materials, such as Trivex and Polycarbonate naturally block most UV light and do not benefit from the application of a UV coating.[citation needed]
Scratch resistance
Highly recommended, especially for polycarbonate and softer materials, to make lenses last longer. This is done automatically by many labs for polycarbonate and high index lenses.
Confusing corrective lens industry terminology
Spheric vs. aspheric, atoric, etc.
Lens manufacturers claim that aspheric lenses improve vision over traditional spheric lenses. This statement could be misleading to individuals who do not know that the lenses are being implicitly compared to "a spheric flattened away from best-form for cosmetic reasons". This qualification is necessary since best-form spherics are always better than aspherics for an ophthalmic lens application.[1] Aspherics for corrective lenses are only[used to attempt to improve the degradation caused by deviating from best-form sphere resulting from making a flatter lens for cosmetic reasons. The same applies for atoric and bi-aspheric.
It is true that aspheric lenses are used in cameras and binoculars. It would be wrong to assume that this means aspherics/atorics are a sign of good optics in eyewear. Cameras and telescopes use multiple lens elements and have different design criteria. Spectacles are made of only one ophthalmic lens. The best-form spheric lens has been shown to give the best vision. In cases where best-form is not used, such as cosmetic flattening, thinning, or wrap-around sunglasses, an aspheric design can reduce the amount of induced optical distortions.
The problem with aspheric lenses is that they are a broad category. A lens is made of two curved surfaces, and an aspheric lens is a lens where one or both of those surfaces is not spherical. Further research and development is being conducted to determine if the mathematical and theoretical benefits of aspheric lenses can actually lead to better vision correction.
Optical aberrations of the eye lens vs. corrective lens
Optical terms are used to describe error in the eye's lens and the corrective lens. This can cause confusion, since "astigmatism" or "ABBE" has drastically different impact on vision depending on which lens has the error.
Astigmatism disambiguation
Astigmatism of the eye: People prescribed a sphere and a cylinder prescription have astigmatism of the eye and can be given a toric lens to correct it.
Astigmatism of the corrective lens: This phenomenon is called lens-induced oblique astigmatism error (OAE) or power error and is induced when the eye looks through the ophthalmic lens at a point oblique to the optical center (OC). This may become especially evident beyond -6D.
Example: A patient with astigmatism (or no astigmatism) of the eye and a high prescription may notice astigmatism of the lens (OAE) when looking through the corner of their glasses.
Aspheric and atoric disambiguation
An ophthalmic "aspheric lens" specifically refers to a subclass of aspheric lens. Designs referring to "flatter" curves are trading off optical quality for cosmetic appearance. An aspheric lens attempts to correct the error induced by flattening the lens by using a non-spheric lens shape. Typically the design focuses on reducing the error (OAE) across the horizontal and vertical lens axis edges. This can be primarily beneficial to farsighted individuals, whose lenses have a thick center.
An atoric lens design refers to a lens with more complex aspheric lens design. An atoric lens design can address error over more corners of the lens, not just the horizontal and vertical axis.
"A toric" (two words, not "atoric") lens is a lens designed to compensate for the patients with astigmatism in their eye. Even though this technically requires an "aspheric" lens, "aspheric" and "atoric" are reserved for lenses which correct errors induced by cosmetic lens flattening.




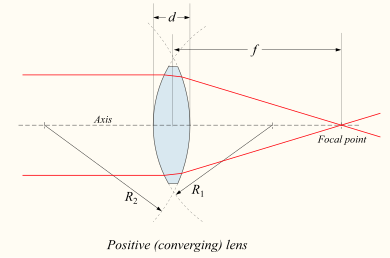

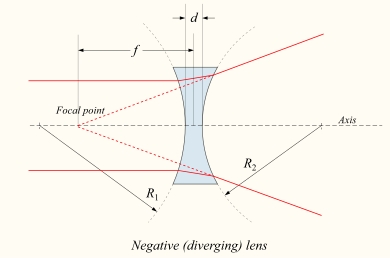

![\frac{1}{f} = (n-1) \left[ \frac{1}{R_1} - \frac{1}{R_2} + \frac{(n-1)d}{n R_1 R_2} \right],](http://upload.wikimedia.org/math/d/5/d/d5d9b5b95cf3fd9ea7f2549ae4ee8fa6.png)
![\frac{1}{f} \approx \left(n-1\right)\left[ \frac{1}{R_1} - \frac{1}{R_2} \right].](http://upload.wikimedia.org/math/a/f/a/afad8f375f5846cea8f9e8091f145d60.png)


 .
.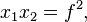

 ,
,